목표
- 다양한 데이터의 종류를 이해
- 편차, 분산, 표준편차의 개념을 이해
- 표본분포와 히스토그램의 개념을 학습
- 신뢰구간과 정규분포의 개념을 익히고 응용
≣ 목차
01. 데이터의 종류
- 데이터 분석에 사용되는 통계
| 구분 | 상세 |
| 분석 기법 | * 기초 통계분석 * 상관분석 * 회귀분석 * 분류분석 * 군집분석 * RFM 분석 |
| 분석 방법론 | * A/B TEST |
| 통계이론 | * 기초통계이론(평균, 분산, 표준편차) * 정규분포와 중심극한정리 * 신뢰구간과 유의수준 * 가설 설정 * 통계적 유의성 검정 * 통계적 가설 검정 |
- 데이터의 종류
| 데이터 종류 | 개념 | 예시 |
| 수치형 | 숫자를 이용해 표현할 수 있는 데이터 이산형, 연속형을 모두 포함하는 개념 |
체중, 신장, 사고선수, 일 방문자수 |
| 연속형 | 일정 범위 안에서 어떤 값이든 취할 수 있는 데이터 | 체중, 신장 |
| 이산형 | 횟수와 값은 정수형 값만 취할 수 있는 데이터 즉, 소수점의 의미가 없는 데이터를 의미(수치형 데이터와의 차이점) |
사고건수, 일 방문자수 |
| 범주형 | 가능한 범주 안의 값만을 취하는 데이터 = 값이 달라짐에 따라 좋거나 나쁘다고 할 수 없는 데이터 = 명목형 이진형, 순서형을 모두 포함하는 개념 |
나라, 도시, 혈액형 성공여부, 등수, MBTI |
| 이진형 | 두 개의 값만을 가지는 범주형 데이터의 특수한 경우 * 0과 1 * 예 / 아니오 * 참 / 거짓 |
성별 성공여부 |
| 순서형 | 값들 사이에 분명한 순위가 있는 데이터 | 등수 |

02. 편차, 분산, 표준편차, 표본분포
- 평균: 모든 값의 총 합을 개수로 나눈 값 ( 34/5 = 6.8 )
- 중간값: 데이터 중 가운데 위치한 값 ( 5 개 중 중간에 위치한 6 )
- 최빈값: 데이터 중 가장 많이 도출된 값 ( 6 이라는 숫자가 2번 있으므로 6 )
- 평균, 중앙값, 최빈값은 데이터의 'WHERE = (어디에 존재하는가)'를 표현하는 개념
- 편차, 분산, 표준편차
- 분산과 편차는 'HOW = 어떻게 존재하는가'에 대한 개념
- 편차(deviation): 하나의 값에서 평균을 뺀 값 = 평균으로부터 얼마나 떨어져 있는지를 의미
- 분산(variance): 편차의 합이 0으로 나오는 것을 방지하기 위해 생성된 개념 = 편차 제곱합의 평균
- 표준편차: 분산에 제곱근을 씌워준 값. (=원래 단위로 되돌리기 = standard deviation(σ))
- 모집단, 표본, 표본분포
- 모집단: 어떤 데이터 집합을 구성하는 전체 대상
- 표본: 모집단 중 일부. 모집단의 부분집합
- 표본분포: 표본의 분포. 표본이 흩어져 있는 정도. 표본통계량으로부터 얻은 도수분포
- 표본평균의 분포: 모집단에서 여러 표본을 추출하고 각 표본의 평균을 계산한다면, 이는 중심극한정리에 따라 정규분포에 가까워집니다. 이는 표본 크기가 충분히 크다면 표본 평균이 정규분포를 따른다는 것을 의미합니다.
- 표본분산의 분포: 모집단에서 여러 표본을 추출하고 각 표본의 분산을 계산한다면, 이 표본분산들의 분포는 카이제곱 분포(다음강의에서 설명)를 따릅니다. 이는 모집단이 정규분포를 따를 때 보다 높게 성립됩니다.
- 표준오차: 표본의 표준편차. = 표본평균의 평균과 모평균의 차이
- 모집단에서 표본을 추출하고, 이를 시각화하여 통계적 의미를 찾기
- 도수: 특정 구간에 발생한 값의 수
- 상대도수: 특정 도수를 전체 도수로 나눈 비율
- 도수분포표: 각 값에 대한 도수와 상대도수를 나타내는 표
- 히스토그램: 도수분포표를 활용하여 만든 막대그래프 😄
- 임의표본추출: 무작위로 표본을 추출하는 것
- 편향: 한쪽으로 치우쳐져 있음
| 순서 | 내용 |
| 1 | 최댓값, 최솟값, 계산 |
| 2 | 최댓값, 최솟값을 포함하여 데이터를 특정 범위(계급)으로 나눔 |
| 3 | 각 계급을 대표하는 수치(계급값) 정하기 |
| 4 | 각 계급에 포함된 데이터 개수(도수)를 카운트 |
| 5 | 각 계급의 도수가 전체에서 차지하는 비율(상대도수)을 계산 |
| 6 | 특정 계급까지의 도수를 모두 sum(누적도수) |
03. 정규분포, 신뢰구간
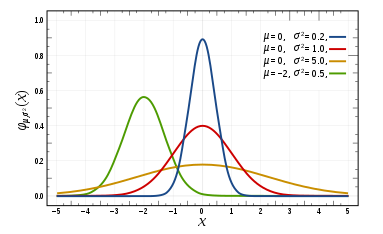
- 정규분포 특징
- 분포는 평균을 중심으로 좌우 대칭의 형태.
- 곡선은 각 확률값을 나타내며, 모두 더하면 1. (동전을 뒤집어서 앞면이 나올 확률은 2분의 1 + 뒷면이 나올 확률 2분의 1 = 전체 확률 1)
- 정규분포는 평균과 분산(퍼진정도)에 따라 다른 형태를 가진다
- 평균 0, 분산 1을 가지는 경우, 이는 표준정규분포. (그림의 붉은색 그래프)
- 표준화
- standard scaler 공식: 확률변수 X(값)에서 평균 m을 빼고 표준편차로 나눈 값
- 데이터분석시 표준화가 필요한 경우: 머신러닝 모델을 만들 때 / 데이터의 범위가 많이 차이나는 경우
- 신뢰구간: 특정 범위 내에 값이 존재할 것으로 예측되는 영역
- 신뢰수준: 실제 모수를 추정하는데 몇 퍼센트의 확률로 신뢰구간이 실제 모수를 포함하게 되는 확률. 주로 95%와 99% 이용
- 신뢰수준 95% : 무작위로 표본을 추출했을 때, 100번 중 95번은 모집단의 값을 포함
- 신뢰수준 99% : 무작위로 표본을 추출했을 때, 100번 중 99번은 모집단의 값을 포함
- 신뢰수준이 높아지게 되면 → 신뢰구간이 넓어지지만 → 정확한 예측이 어렵기 때문에, 95% 신뢰수준보다 99% 신뢰수준이 좋다고 할 수 없다.
'[업무 지식] > Statistics' 카테고리의 다른 글
| [카이제곱검정] 가설검정 (0) | 2024.11.16 |
|---|---|
| [통계적 실험] (1) | 2024.11.14 |
| [선형관계확인] 다양한 방법 (0) | 2024.11.12 |
| [상호정보 상관계수] 상호정보를 이용한 변수끼리의 계산 (0) | 2024.11.12 |
| [비모수상관계수] 상관관계 (0) | 2024.11.12 |



